
Tanta ausiliari! dal sarpra a tramonto appanni di aa astro «oalsiasi alla tatitndiia
L’ora I* (civile — T. M. E. C
dato istante, è data da:
te
= *« + *« — *,» + (X/— X)
) di un astro, per un
(
1
)
ove t« (tempo astro) = 12* —
P
per astro a levante e
12
+
P
per astro a ponente;
x« è
l’ascensione retta del
l’astro; amè l’a. r. del Sole medio e X/— X la differenza
tra la longitudine del meridiano centrale del fuso nel
quale è compreso il luogo di osservazione e X che è la
longitudine del luogo stesso.
Se ci limitiamo al caso particolare del sorgere e tra
monto, l’arco semidiurno (angolo al polo P ), tenuto conto
della rifrazione, vien espresso da:
_ cos 90° 34'.9— sin o sin
8
...
cos
P
= ---------------------- ^----------
(i)
tabulati i valori di P, ovvero di
t,
(v. sopra), i quali
costituiscono, con l’aggiunta sistematica di X/— X= 28",9
per Pino Torinese, Torino (29m,2) e dintorni, la pre
sente Tavola ausiliaria.
Dunque nella determinazione di I si adopera la Tav. A
se la declinazione dell’astro è boreale o + , e la Tav. B se $
è australe o —. Al valore dato dalla Tavola si aggiunge a.
ed alla somma si toglie oc,,. Questi due valori si trovano
in qualsiasi annuario; son preferibili le
Effemeridi astro
nomiche
dell’istituto Idrografico di Genova.
Nel caso del Sole, volendo determinare il sorgere o il
tramonto con approssimazione maggiore di quella dei
dati della Nota precedente, la relazione (1) diventa:
te =
I, - f a . — a * + (X/ — X)
cos
9
cos
8
Se poi ci riferiamo solo a un determinato luogo, per
es. Torino, come nel nostro caso, dalla formola (2) si vede
che l’unico valore che cambia è S (declinazione dell’astro).
Facendo quindi variare
8
da 0° a 45°, essendo la latitu
dine (
9
) di Torino (Pino Torinese) = 45° 2' 16''.3, si sono
-------
. .
.
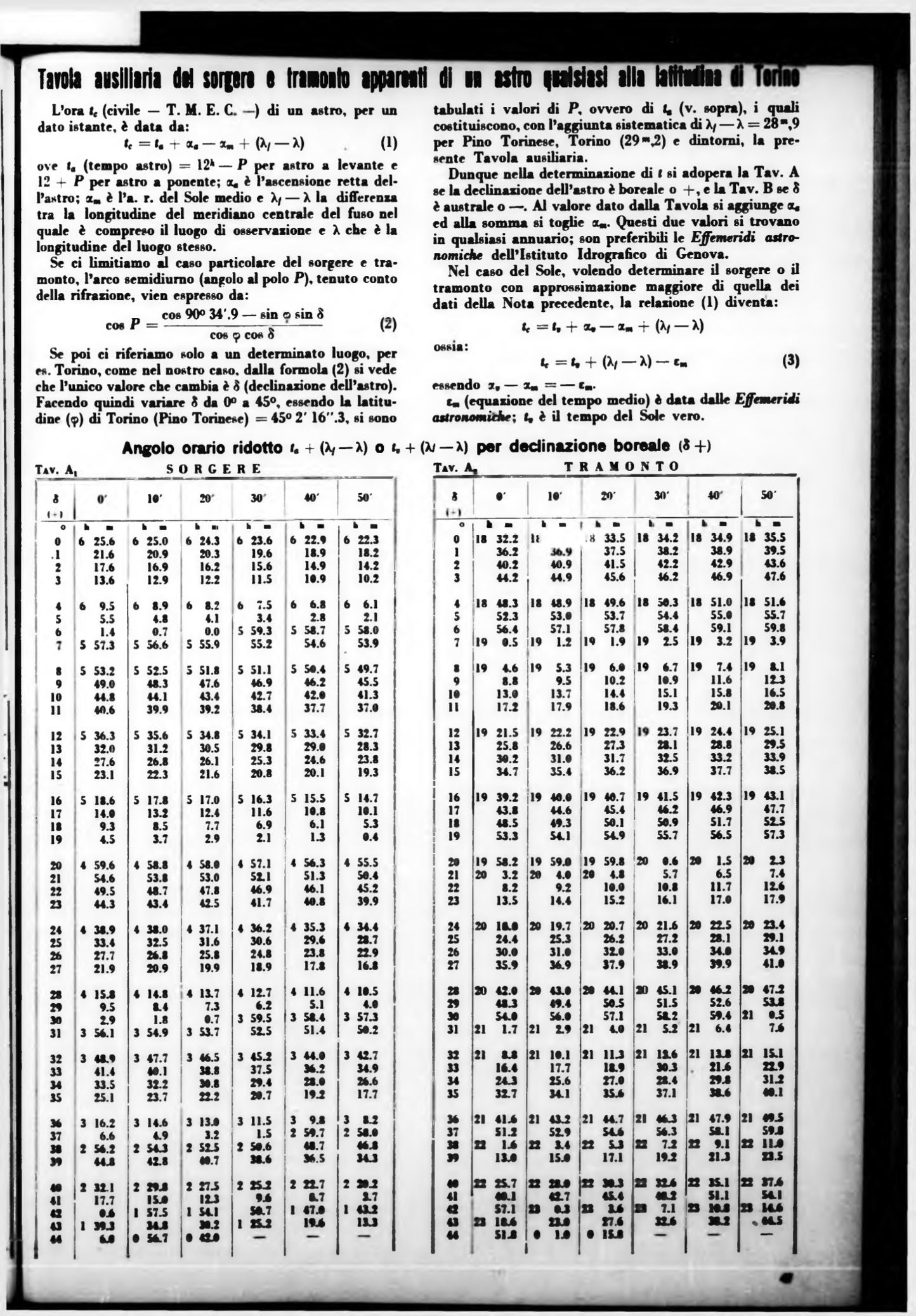
À n g o l o o r a r io r id o t t o
u
+ (X/ — x) o t, + (xy — x) p e r d e c l i n a z i o n e b o r e a l e (8 + )
S O R G E R E
T
av
. A.
T R A M O N T O
ossia:
te
= I» + (X/— X) — Cm
(3)
essendo x, —
x » =
— e*.
tm
(equazione del tempo medio) è data dalle
Effemeridi
astronomiche
; t» è il tempo del Sole vero.
T
av
.
A,
4
( 1
10
'
20
30 40'
50'
0 b
08
b m b
di
b m b m b
m
0 6
25.6
6
25.0
6
24.3
6
23.6
6
22.9
6
22.3
.1
21.6
20.9 20.3 19.6 18.9 18.2
2
17.6 16.9 16.2 15.6 14.9 14.2
3 13.6 12.9
12.2
11.5 10.9
10.2
4
6
9.5
6
8.9
6 8.2 6
7.5
6 6.8 6 6.1
5 5.5 4.8 4.1 3.4
2.8
2.1
6
1.4 0.7
0.0
5 59.3 5 58.7 5 58.0
5
57.3 5 56.6 5 55.9 55.2 54.6
*
53.9
8
5 53.2 5 52.5 5 51.8 5 51.1
5
50.4 5 49.7
9 49.0 48.3 47.6 46.9 46.2 45.5
10
44.8 44.1 43.4 42.7 42.0 41.3
11
40.6 39.9 39.2 38.4 37.7 37.0
12
5 36.3 5 35.6 5 34.8 5 34.1 5 33.4 5 32.7
13 32.0 31.2 30.5 29.8 29.0 28.3
14 27.6 26.8 26.1 25.3 24.6 23.8
15 23.1 22.3
21.6 20.8 20.1
19.3
16 5 18.6 5 17.8 5 17.0 5 16.3 5 15.5 5 14.7
. 17 14.0 13.2 12.4
11.6 10.8 10.1
18 9.3 8.5 7.7 6.9
6.1
5.3
19 4.5 3.7 2.9
2.1
1.3 0.4
20
4 59.6 4 58.8 4 58.0 4 57.1 4 56.3 4 55.5
21
54.6 53.8 53.0 511 51.3 50.4
22
49.5 48.7 47.8 46.9 46.1 45.2
23 44.3 43.4 42.5 41.7 40.8 39.9
24 4 38.9 4 38.0 4 37.1 4 36.2 4 35.3 4 34.4
25 33.4 32.5 31.6 30.6 29.6 28.7
26 27.7 26.8 25.8 24.8 23.8 22.9
27 21.9 20.9 19.9 18.9 17.8 16.8
28 4
ISJ
4 14.8 4 13.7 4 12.7 4
11.6
4 10.5
29 9.5 8.4 7.3
6.2
S
.1
4.0
30 2.9
1.8
0.7 3 59.5 3 50.4 3 57.3
31
3
56.1 3 54.9 3 53.7 515 51.4 50.2
32 3 48.9 3 47.7 3 46.5 3 45.2 3 44.0 3 42.7
33 41.4 40.1 38.8 37.5 36.2 34.9
34 33.5 32.2 30.8 29.4
20.0
26.6
35 25.1 23.7
22.2
20.7 19.2 17.7
36 3 16.2 3 14.6 3 I3J 3 11.5 3 9.8 3
1.2
37
6.6
4.9 3.2 1.S
2
59.7
2
58.0
38
2 56.2 2
54.3
2
52.5
2
50.6 40.7 46J
»
44.8 42.8
40.7
38.6 36.5 34.3
\
40 2
32-1
2 »
2 27.S 2 2S.2 2 217 2 28.2
«1 17.7 130 113
9.6
17
17
42
0.4 1 57.5
1
SAI
50.7
1
47.0
1
412
41
1
39J 34J 38.2
1
212
1 *
j ì
113
44
U
!
0 56.7 0 410
»
1
.
0
'
10
'
20
'
30'
40
1
50'
o
k
■a
k m
m 1 m l
OD
m
0
18 32.2
n
.8
33.5 18 34.2 18 34.9 18 35.5
1
36.2
37.5 38.2 38.9 39.5
2
40.2 40.9 41.5 42.2 42.9 43.6
3 44.2 44.9 45.6 46.2 46.9 47.6
4 18 48.3 18 48.9 18 49.6 18 50.3 18 51.0 18 51.6
5 52.3 53.0 53.7 54.4 55.0 S5.7
6
56.4 57.1 57.8 58.4 S9.1 59.8
7 19 0.5 19
1.2
19 1.9 19 2.5 19 3.2 19 3.9
8
19 4.6 19 5.3 19
6.0
19 6.7 19 7.4 19
11
9
8.8
9.5
10.2
10.9
11.6
113
10
13.0 13.7 14.4 15.1 15.8 16.5
11
17.2 17.9 18.6 19.3
20.1
20.8
12
19 21.5 19
22.2
19 22.9 23.7 19 24.4 19 25.1
13 25.8 26.6 27.3 28.1 28.8 29.5
14 30.2 31.0 31.7 32.5 33.2 33.9
15 34.7 35.4 36.2 36.9 37.7 38.5
16 19 39.2 19 40.0 19 40.7 19 41.5 19 42.3 19 43.1
17 43.8 44.6 45.4 46.2 46.9 47.7
18 40.5 49.3 50.1 50.9 51.7 SIS
19 53.3 54.1 54.9 55.7 56.5 S7.3
20
19 58.2 19 59.0 19 59.8
20 0.6 20
1.5
20
13
21 20
3.2
20
4.0
20
4.8 5.7 6.5 7.4
22
8.2
9.2
10.0 10.8
11.7 116
23 13.5 14.4 15.2 16.1 17.0 17.9
24
20 110 20
19.7
20
20.7
20 21.6 20
215
20
23.4
25 24.4 25.3 26.2 27.2 28.1 29.1
26 30.0 31.0 310 33.0 34.0 34.9
27 35.9 36.9 37.9 38.9 39.9 41.0
28
20
42.0
20
410
20
44.1
20
45.1
20
46J
20
47.2
29 48.3 49.4 S0.S 51.S 52.6 SIS
30 54.0 56.0 57.1 512 S9.4
21
0.5
31
21
1.7
21
19
21
4.0
21
S .2
21
6.4 7.6
32
21 10 21 10.1 21
11.3
21
116
21
118
21 111
33 16.4 17.7 119 30.3
21.6
219
34 24.3 25.6 27.0 28.4 29J 31.2
35 317 34.1 3S.6 37.1 316 4i.l
36
21
4M
21
412
21
44.7
21
46J
21
47.9
21
49.5
37 51.2 519 SU 56.3 511 S9J
38
22 1.6 22
14
22
13
22
7.2
22
9.1
22
ua
39
110
1S.0 17.1 19.2
21
J 23.5
40
22
217
22
204
22
313
22
316
22
311
22
37
j
6
41 40.1 417 414 412 S1.1 54.1
42 S7.1 23
U
23 36 23 7.1 23
10
J 23 Mi
41 23
11
*
210
27.6 316 312
% 44.5
*
sia
0
l i
0
i l i
"
“““


















